https://yjhtpi.tistory.com/345
여기서 상보필터의 내용만 다시 복붙.
아래 이미지는 상호보완 필터의 개념도 입니다.

상보필터(상호보완) 개념도
[ 상보필터의 원리 - Complementary Filter ]
- 가속도 센서(Accelerometer)는 센서 특성상 고주파 영역에서 노이즈가 많이 발생하게 되어 정확한 값을 얻기 어려운데요, 그래서 노이즈 영역을 제거하고자 고역은 감쇠시키고, 낮은 주파수 영역을 통과시키는 저역필터(Low Pass Filter)를 적용해주면 정확도가 올라갑니다.
- 자이로 센서(Gyroscope)는 센서 특성상 저주파 영역에서 값이 변하는 Drift현상이 발생하여 정확한 값을 기대하기가 어렵습니다. 그래서 저역을 감쇠시키고 노이즈가 적은 고역을 통과시키기 위한 고역필터(High Pass Filter)를 적용해주면 역시 정확도가 올라갑니다.
※ 이렇게 각각의 필터를 통과해서 노이즈가 걸러진 값들을 합하여 보다더 정확한 각도값을 얻게 됩니다.
이외에 칼만필터(Kalman Filter), Quanternion 라는 것도 있습니다.
상보필터에서는 가속도 센서의 저주파 영역에서의 장점과 , 자이로센서의 고주파 영역에서의 장점만을 융합한 필터로서 , 방법과 코드가 간단하여 적용하기 쉬운 장점이 있습니다. 상보필터에서는 ALPHA라는 가중치 값을 통해 자이로센서와 가속도센서 각각으로부터 얻은 각도를 어떤 비중으로 적용시킬지 정하여 계산하게 되는데요.
아래가 바로 보정값(가중치) ALPHA를 적용한 보정된 각도 값의 식(angleFiX) 입니다.
angleFiX = ALPHA * angleTmpX + (1.0 - ALPHA) * angleAcX;
여기서 angleTmp 는 자이로센서 값을 기준으로 만든 상보필터 처리를 위한 임시각도이며
X축에 대해 정리하면 angleTmpX = angleFiX + angleGyX * dt 가 됩니다.
가중치 ALPHA 값은 α = T/(T+Δt) 식으로 구하는데요, α (ALPHA) = 1 / (1+0.04) 가되어, α 값은 0.96 이 됩니다.
즉, 1(T) 사이클 도는 동안의 loop Time(Δt=0.04) 을 적용한 식입니다. 그런데 이 값은 고정값은 아니며, loop Time이 길어지거나 등의 이유로 알파값을 시스템에 맞게 변경할 수 있습니다.
즉, angleFiX 식을 보면 아시겠지만, 자이로 값에 * 0.96 가중치를 곱하고(주고), 가속도 값에 * 0.04의 가중치를 줘서 합한 값이어서 자이로센서(자이로스코프)에 더 의존하는 형태라고 말 할 수 있습니다. 그런데, 이런 형태가 비교적 정밀한(안정적인) 출력값을 내는 이유는, 식을 다시 살펴보면
angleFiX = ALPHA * angleTmpX + (1.0 - ALPHA) * angleAcX;
각도 변화가 상당히 느린 구간(저주파 영역)에서는 자이로센서의 데이터 값이 작아지기 때문에(angleGyX * dt의 누적값 감소), (1.0-ALPHA) = 0.04 가중치 적용으로 작았던 가속도 데이터 값이 상대적으로 커지게 되어 , 자이로스코프의 저주파 영역에서 발생하는 Drift(드리프트)에 대한 단점을 보완 할 수 있게 됩니다.
▶ 아두이노 코드
( 위에서 설명한 식을 코드에 적용한 아두이노 코드입니다. 실습 #1과 실습#2에 소개한 코드를 합쳐서, 상보필터 식을 적용한 코드입니다. 축 3가지를 동시에 시리얼모니터로 확인하기 불편하기 때문에, 일부 축에 주석처리 되어 있으니, 필요한 경우 주석을 해제하여 사용하세요. )
- 시리얼모티너(플로터) 출력은 아래처럼 각 축별로 비교하기 쉽도록 배치하였습니다.
《가속도센서 X축》 출력과 《필터링된 X축》 출력
《가속도센서 Y축》 출력과 《필터링된 Y축》 출력
《자이로센서 Z축》 출력과 《필터링된 Z축》 출력
// 《 상보필터를 적용한 Roll과 Pitch, Yaw의 각도 구하기 실습 》
/* 아래 코드관련 실습에 대한 설명과 회로도 및 자료는 https://rasino.tistory.com/ 에 있습니다 */
#include<Wire.h>
const int MPU_ADDR = 0x68; // I2C통신을 위한 MPU6050의 주소
int16_t AcX, AcY, AcZ, Tmp, GyX, GyY, GyZ; // 가속도(Acceleration)와 자이로(Gyro)
double angleAcX, angleAcY, angleAcZ;
double angleGyX, angleGyY, angleGyZ;
double angleFiX, angleFiY, angleFiZ;
const double RADIAN_TO_DEGREE = 180 / 3.14159;
const double DEG_PER_SEC = 32767 / 250; // 1초에 회전하는 각도
const double ALPHA = 1 / (1 + 0.04);
// GyX, GyY, GyZ 값의 범위 : -32768 ~ +32767 (16비트 정수범위)
unsigned long now = 0; // 현재 시간 저장용 변수
unsigned long past = 0; // 이전 시간 저장용 변수
double dt = 0; // 한 사이클 동안 걸린 시간 변수
double averAcX, averAcY, averAcZ;
double averGyX, averGyY, averGyZ;
void setup() {
initSensor();
Serial.begin(115200);
caliSensor(); // 초기 센서 캘리브레이션 함수 호출
past = millis(); // past에 현재 시간 저장
}
void loop() {
getData();
getDT();
angleAcX = atan(AcY / sqrt(pow(AcX, 2) + pow(AcZ, 2)));
angleAcX *= RADIAN_TO_DEGREE;
angleAcY = atan(-AcX / sqrt(pow(AcY, 2) + pow(AcZ, 2)));
angleAcY *= RADIAN_TO_DEGREE;
// 가속도 센서로는 Z축 회전각 계산 불가함.
// 가속도 현재 값에서 초기평균값을 빼서 센서값에 대한 보정
angleGyX += ((GyX - averGyX) / DEG_PER_SEC) * dt; //각속도로 변환
angleGyY += ((GyY - averGyY) / DEG_PER_SEC) * dt;
angleGyZ += ((GyZ - averGyZ) / DEG_PER_SEC) * dt;
// 상보필터 처리를 위한 임시각도 저장
double angleTmpX = angleFiX + angleGyX * dt;
double angleTmpY = angleFiY + angleGyY * dt;
double angleTmpZ = angleFiZ + angleGyZ * dt;
// (상보필터 값 처리) 임시 각도에 0.96가속도 센서로 얻어진 각도 0.04의 비중을 두어 현재 각도를 구함.
angleFiX = ALPHA * angleTmpX + (1.0 - ALPHA) * angleAcX;
angleFiY = ALPHA * angleTmpY + (1.0 - ALPHA) * angleAcY;
angleFiZ = angleGyZ; // Z축은 자이로 센서만을 이용하열 구함.
Serial.print("AngleAcX:");
Serial.print(angleAcX);
Serial.print("\t FilteredX:");
Serial.print(angleFiX);
Serial.print("\t AngleAcY:");
Serial.print(angleAcY);
Serial.print("\t FilteredY:");
Serial.println(angleFiY);
Serial.print("\t AngleAcZ:");
Serial.print(angleGyZ);
Serial.print("\t FilteredZ:");
Serial.println(angleFiZ);
// Serial.print("Angle Gyro X:");
// Serial.print(angleGyX);
// Serial.print("\t\t Angle Gyro y:");
// Serial.print(angleGyY);
// Serial.print("\t\t Angle Gyro Z:");
// Serial.println(angleGyZ);
// delay(20);
}
void initSensor() {
Wire.begin();
Wire.beginTransmission(MPU_ADDR); // I2C 통신용 어드레스(주소)
Wire.write(0x6B); // MPU6050과 통신을 시작하기 위해서는 0x6B번지에
Wire.write(0);
Wire.endTransmission(true);
}
void getData() {
Wire.beginTransmission(MPU_ADDR);
Wire.write(0x3B); // AcX 레지스터 위치(주소)를 지칭합니다
Wire.endTransmission(false);
Wire.requestFrom(MPU_ADDR, 14, true); // AcX 주소 이후의 14byte의 데이터를 요청
AcX = Wire.read() << 8 | Wire.read(); //두 개의 나뉘어진 바이트를 하나로 이어 붙여서 각 변수에 저장
AcY = Wire.read() << 8 | Wire.read();
AcZ = Wire.read() << 8 | Wire.read();
Tmp = Wire.read() << 8 | Wire.read();
GyX = Wire.read() << 8 | Wire.read();
GyY = Wire.read() << 8 | Wire.read();
GyZ = Wire.read() << 8 | Wire.read();
}
// loop 한 사이클동안 걸리는 시간을 알기위한 함수
void getDT() {
now = millis();
dt = (now - past) / 1000.0;
past = now;
}
// 센서의 초기값을 10회 정도 평균값으로 구하여 저장하는 함수
void caliSensor() {
double sumAcX = 0 , sumAcY = 0, sumAcZ = 0;
double sumGyX = 0 , sumGyY = 0, sumGyZ = 0;
getData();
for (int i=0;i<10;i++) {
getData();
sumAcX+=AcX; sumAcY+=AcY; sumAcZ+=AcZ;
sumGyX+=GyX; sumGyY+=GyY; sumGyZ+=GyZ;
delay(50);
}
averAcX=sumAcX/10; averAcY=sumAcY/10; averAcZ=sumAcY/10;
averGyX=sumGyX/10; averGyY=sumGyY/10; averGyZ=sumGyZ/10;
}《 위 코드 다운로드 》
※ 아래 실행결과 화면을 보시면 알겠지만, 상보필터를 적용 후의 그래프는 노이즈나 한 번씩 크게 튀는 값 들이 상당히 제거되어 나타나는 것을 알 수 있습니다. 단, 노이즈 향상을 위해 ALPHA값 등, 보정값을 과도하게 조정하게 되면, 보정된 데이터의 출력 딜레이(시간차)가 발생하게 됩니다. 이는 드론(Drone)과 같은 제어에 있어서는 적시에 올바른 제어를 할 수 없게 만들 수도 있습니다.
▶ 실행 결과
1. 《가속도센서 X축》 출력과《필터링된 X축》 출력 비교 화면
먼저, 시리얼모니터 화면을 살펴 보세요.(아래 이미지) , 보드를 77도 정도에서 고정한 상태에서 가속도센서에서 얻은 데이터는 각도 값이 68~70도 사이를 짧은 순간에 제법 심하게 요동치고 있는 반면에, 필터링한 각도 값은, 77도에서 소수점 단위 정도만 변동이 있을 뿐 매우 안정된 출력을 보여주고 있는 것을 알 수 있습니다.

그럼, 이제 시리얼 모니터만으로는 잘 체감이 안 되실텐데요, 같은 출력을 아두이노 IDE 메뉴에 있는 '시리얼 플로터'를 통해 그래프로 보면 좀더 확연히 그 차이를 구분하실 수 있게 됩니다. (아래)
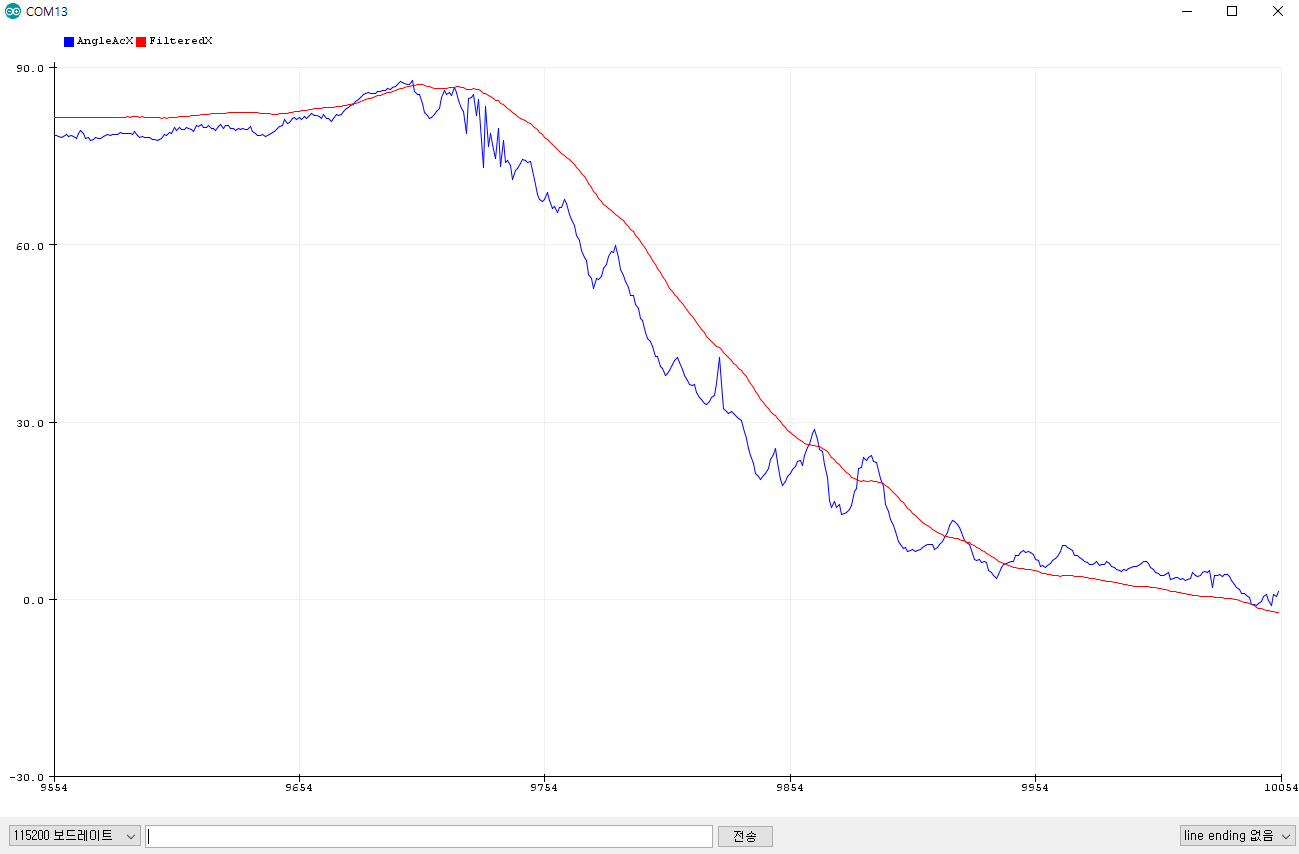
파란색 그래프가 가속도센서로 부터 얻은 X축 회전(각도)상태의 데이터인데요, 떨림과 같은 병동이 심한 반면에,
필터링 코드를 거친 빨간색 X축의 데이터는 이런 노이즈들이 깔끔하게 제거 된 것을 알 수 있습니다.
2. 《가속도센서 Y축》 출력과《필터링된 Y축》 출력 비교 화면
그럼, Y축 그래프도 살펴 볼게요.

역시 마찬가지로, 필터링 되지 않은 Y축 출력과 필터링된 Y축 출력에 차이가 있음을 볼수 있습니다.
3. 《자이로센서 Z축》 출력과《필터링된 Z축》 출력 비교 화면
그리고, Z축 같은 경우는 앞서 설명드린대로, 가속도 센서로부터는 데이터를 얻을 수 없는 상태이고, 따라서 자이로 센서로 부터 얻은 Z축 데이터와, 자이로센서 데이터 가중치가 높은 필터링된 Z축 데이터를 출력해 본 것이어서 두 그래프간의 차이가 거의 없는 그래프 모습을 보여주고 있습니다.

3. 끝으로 전체 축을 동시에 비교해봤습니다. 《자이로센서 X-Y-Z-축》 출력과